Matlab’da Polinomlar

MATLAB ÖZEL DERSİ ALMAK İÇİN TIKLAYIN.

 

Matlab’da Polinom Uygulamaları

Bu bölümde polinomlar ile ilgili Matlab komutlarını göreceğiz. Sırasıyla:

  1. Matlab'da Bir Polinomun Tanıtılması

  2. Matlab'da Polinomun köklerinin bulunması: Matlab roots komutu

  3. Matlab'da Polinomların Toplanması

  4. Matlab'da Polinomların Çarpılması: Matlab conv komutu

  5. Matlab’da Kökleri Bilinen Bir Polinomu Elde Etme: Matlab poly komutu

  6. Matlab’da Bir Matrisin Karakteristik Denkleminin Bulunması: Matlab poly komutu

  7. Matlab’da Polinomda Bilinmeyenin yerine değer atanması: Matlab polyval komutu

  8. Matlab’da Bir Polinomun Türevinin Alınması: Matlab polyder komutu

  9. Matlab’da Bir Polinomun İntegralinin Alınması: Matlab polyint komutu

  10. Matlab’da Polinomial Eğri Uydurulması Matlab polyfit komutu

Bir Polinomun Matlab’a Tanıtılması

P(s)= a s^4 + b s^3 +c s^2+ d s +e - www.matlabakademi.com şeklindeki bir polinomu Matlab’a Tanıtmak için, polinomun katsayılarını kullanacağız. ‘katsayi’ adında bir satır vektör tanımlarsam, Matlab’ta bunu: >> katsayi = [a b c d e] şeklinde girmem gereklidir. Böylelikle katsayılarını satır vektör olarak girdiğim polinom üzerinde Matlab’ın hazır komutlarını kullanarak, polinomların kökünün bulunması, çarpılması gibi işlemleri kolaylıkla yapabileceğiz. Örnek: P(s) = s^4 +2 s^3 + s^2 + 3 s + 6 - www.matlabakademi.com şeklindeki bir polinomu: >> katsayi1 = [1 2 1 3 6] şeklinde Matlab komut ekranından girebiliriz. Matlab’da Polinomun Köklerinin Bulunması: Polinomun köklerini bulmak için ‘roots’ komutunu kullanacağız. Daha önce katsayılarını bir satır vektöre atadığımız Polinomun köklerini aşağıdaki şekillerde Matlab’a buldurabiliriz.

Matlab roots komutu

roots(katsayilar) veya    kokler = roots(katsayilar) Örnek: P(s)= 1 s^{2} + 2 s +1 - www.matlabakademi.com polinomunun köklerinin Matlab yardımıyla bulunması. >> katsayilar = [1 2 1]; >> roots(katsayilar) ans = -1 -1

Örnek:

s^4 - 6 s^3 + 11 s^2 - 6 s - www.matlabakademi.com

polinomunun köklerinin Matlab’da bulunması: >> katsayilar = [1 -6 11 -6 0]; >> kokler = roots(katsayilar) kokler = 0 3.0000 2.0000

1.0000

 Bu örnek’te görüldüğü üzere polinomun kökleri istenirse, bir değişkenine atanabilir. Burada ‘kokler’ isimli değişkene atanmıştır. Polinomun değerleri 0, 3, 2 ve 1’dir. MATLAB KURSU İÇİN TIKLAYIN.

Matlab’da Polinomların Toplanması:

Örnek:

P_1(s) = 3 s^3 + 2 s +1    ve    P_2(s)= 2 s^2 + 10 s + 1   gibi iki polinomu Matlab’da toplamak isteyelim. >> kokler1 = [3 0 2 1]; >> kokler2 = [0 2 10 1]; >> kokler3 = kokler1 + kokler2 kokler3 = 3     2    12     2 İki polinomun toplamı bize P_3(s)= 3 s^3 + 2 s^2 + 12 s +2 polinomunu verecektir. Burada dikkat edilecek husus vektör toplamında boyut eşitliği arandığından 2. polinomun mertebe olarak bulunmayan mertebelerinin katsayılarına sıfır konmuştur. ZOOM üzerinden online canlı özel ders için tıklayın.

Matlab’da Polinomların Çarpılması: (conv)

Matlab conv komutu

Matlab’da polinom çarpımı için ‘conv’ hazır fonksiyonu vardır. Çarpmak istediğimiz polinomların katsayılarını bu fonksiyona girdiğimizde, cevap olarak çarpım sonucu elde edilen polinomun katsayılarını alırız. Örnek: P_1(s)= 3 s^3 + 2 s +1 ve P_2(s)= 2 s^2 + 10 s +1 gibi iki polinomu Matlab’da çarpmak isteyelim. >> kokler1 = [3 0 2 1]; >> kokler2 = [ 2 10 1]; >> kokler3 = conv(kokler1, kokler2) kokler3 = 6    30     7    22    12     1 İki polinomun çarpımı bize  P_3(s)= 6 s^5 + 30 s^4 + 7 s^3 + 22 s^2 +12 s +2   polinomunu verecektir. ‘conv’ hazır fonksiyonu katsayılar dizlerinin eşit boyutta (eşit eleman sayısında) olmasını gerektirmez.

Matlab’da Polinomların Bölünmesi: (deconv)

Matlab deconv komutu

Matlab’da polinom bölümü için ‘deconv’ hazır fonksiyonu vardır. Bölmek istediğimiz polinomların katsayılarını sırasıyla pay ve payda olacak şekilde bu fonksiyona girdiğimizde, cevap olarak bölüm sonucu elde edilen polinomun katsayılarını alırız. ‘deconv’ hazır fonksiyonun kullanım şekli aşağıdaki gibidir. [bolum, kalan]= deconv(bolunen, bolen ) şeklindedir. Örnek: Matlab yardımıyla P_1(s) = 3 s^3 +2 s + 1 polinomunu  P_2(s)= 2 s^2 + 10 s +1 polinomuna bölmek isteyelim. >> kokler1 = [3 0 2 1]; >> kokler2 = [ 2 10 1]; >> [bolum, kalan] = deconv(kokler1, kokler2) bolum = 1.5000   -7.5000 kalan = 0         0   75.5000    8.5000 Yani P_3(s)= \frac{P_1}{P_2}= 1.5 s - 7.5   + \frac{75.5 s +8.5}{2 s^2 + 10 s +1} - www.matlabakademi.com şeklinde olacaktır. MATLAB ÖZEL DERSİ ALMAK İÇİN TIKLAYIN.

Matlab’da Kökleri Bilinen Bir Polinomu Elde Etme: (poly)

Matlab poly komutu:

Matlab’da kökleri bilinen bir polinomun katsayıları ‘poly’ hazır fonksiyonu ile bulunur. Katsayılarını bulmak istediğimiz polinomun köklerini bir satır vektörde tanımlarız. Bu satır vektörü ‘poly’ fonksiyonuna girdiğimizde, cevap olarak polinomun katsayılarını alırız. ‘poly’ fonksiyonu bir nevi ‘roots’ fonksiyonun tersi yönde işlem görür. ‘roots’ fonksiyonu katsayılardan köklere, ‘poly’ fonksiyonu ise köklerden polinom katsayılarına ulaşmamızı sağlar. Örnek: Kökleri -2 ,-3, ve -4 olan polinomu tanımlayınız. Bu polinom P(s) = (s + 2) (s + 3) (s + 4)   şeklinde tanımlanır. >> kokler = [-2 -3 -4]; >> poly(kokler) ans = 1     9    26    2 Yani bu üç ifadenin çarpımıyla elde edilecek polinom P(s) = s^3 + 9 s^2 +26 s + 2 - www.matlabakademi.com Örnek: Kökleri 1-3i ve 1+3i olan polinomu tanımlayınız. >> kokler = [1-3i 1+3i]; >> poly(kokler) ans = 1    -2    10 Yani P(s) = s^2 - 2 s + 10 - www.matlabakademi.com MATLAB KURSU İÇİN TIKLAYIN.

Matlab’da Bir Matrisin Karakteristik Denkleminin Bulunması: (poly)

Matlab poly komutu

A bir matris olmak üzere det(sI-A)= 0 denklemi bize matrisin karakteristik denklemini verir. Matlab’da bir matrisin karakteristik denklemini ‘poly’ hazır fonksiyonu ile buluruz. Genel kullanım formu: Karakteristik_polinom = poly(matris) şeklindedir. Örnek: A = \begin{bmatrix} 0 & 1 \\ 3 &5 \end{bmatrix} matrisinin karakteristik denklemini bulalım. >> A = [0 1 ; 3 5]; >> poly(A) ans = 1.0000   -5.0000   -3.0000

Matlab’da Polinomda Bilinmeyenin yerine değer atanması: (polyval)

Matlab polyval komutu

Matlab’da polinomda bilinmeyenin yerine bir değerin atanması için ‘polyval’ fonksiyonunu kullanılır. Bu fonksiyonum genel kullanım şekli şu şekildedir. polinomun_degeri = polyval(katsayilar, atanacak_deger) Örnek: P(s) = s^5 + 4 s^3 + 2 s^2    ise z = P(10) değeri nedir? >>  katsayilar = [1 0 4 2 0  0]; >> z =polyval(katsayilar, 10) z = 104200  

Matlab’da Bir Polinomun Türevinin Alınması: (polyder)

Matlab polyder komutu

Matlab’da bir polinomun türevini almak için  ‘polyder’ hazır fonksiyonu vardır. Türevini almak istediğimiz  polinomun katsayılarını bir satır vektöre atarız. Bu satır vektörü , ‘polyder’ fonksiyonuna girdiğimizde cevap olarak, polinomun türevi alınmasıyla elde edilen polinomun katsayılarını verecektir. Örnek: P(s) = s^5 + 4 s^3 + 2 s^2 - www.matlabakademi.com fonksiyonun türevini Matlab yardımıyla bulunuz. >> katsayilar = [1 0 4 2 0  0]; >> turev = polyder(katsayilar) turev = 5     0    12     4     0 Yani P(s) = s^5 + 4 s^3 + 2 s^2  polinomunun türevi P(s) = 5 s^4 + 12 s^2 + 4 s  dir. Genel olarak bir polinomun türevini almak kolaydır. Belki bunun için Matlab’a çok ihtiyaç duymaya biliriz. Ancak iki polinomun çarpımını türevini elle almak daha zahmetlidir. Neyse ki bu işlemi de Matlab’a kolaylıkla yaptırabiliyoruz. Örnek: P_1(s) = 3 s^3 + 2 s + 1   ve P_2(s) = 2 s^2 + 10 s +1 - www.matlabakademi.com gibi iki polinomun çarpımının türevini Matlab yardımıyla bulalım. >> katsayi1 = [3 0 2 1]; >> katsayi2 = [ 2 10 1]; >> turev = polyder(katsayi1, katsayi2) turev = 30   120    21    44    12 Alternatif Çözüm: >> katsayi1 = [3 0 2 1]; >> katsayi2 = [ 2 10 1]; >> katsayi = conv(katsayi1, katsayi2); >> turev = polyder(katsayi) turev = 30   120    21    44    12 P(s) = P_1(s) P_2(s) - www.matlabakademi.com polinomunun türevi \frac{dP(s)}{ds} = 30 s^4 + 120 s^3 + 21 s^2 + 44 s + 12 - www.matlabakademi.com dır. ZOOM üzerinden online canlı özel ders için tıklayın.

Matlab’da Bir Polinomun İntegralinin Alınması: (polyint)

Matlab polyint komutu

Matlab’da bir polinomun integralini almak için  ‘polyint’ hazır fonksiyonu vardır. İntegralini almak istediğimiz  polinomun katsayılarını bir satır vektöre atarız. Bu satır vektörü , ‘polyint’ fonksiyonuna girdiğimizde cevap olarak, polinomun integrali alınmasıyla elde edilen polinomun katsayılarını verecektir. Örnek: P_1(s) = 3 s^2 + 2 s +1 - www.matlabakademi.com polinomunun integralini Matlab yardımıyla bulalım. >> kokler1 = [3 2 1]; >> integral = polyint(kokler1) integral = 1     1     1     0 \int 3 s^2 + 2 s + 1 \mathrm{d}x = s^3 + s^2 + s - www.matlabakademi.com şeklinde olacaktır. Denklemden de görüldüğü üzere integral sabiti default olarak 0 alınmıştır. Eğer sıfırdan başka bir integral sabiti denkleme girilmek isteniyorsa, bu fonksiyonda ikinci bir parametre olarak girilebilir. Örnek: >> integral = polyint(kokler1,3) integral = 1     1     1     3 Görüldüğü üzere ‘polyint’ hazır fonksiyonunda girilen ikinci parametre ile integral sabiti olarak 3 olarak girilmiş oldu. Yani \int 3 s^2 + 2 s + 1 \mathrm{d}x = s^3 + s^2 + s + 3 olarak bulmuş olduk.  

Matlab’da Polinomial Eğri Uydurulması (polyfit)

Matlab polyfit komutu

Bir dinamik sistemimiz varsa ve bu sisteme çeşitli girişler uygulayıp çıktıları ölçüyorsak, bu veriler ile giriş ve çıkış arasındaki ilişkiyi polinom olarak ifade edebiliriz. Genel kullanım yapısı aşağıdaki gibidir. polyfit(giris_verileri, cikis_verileri, polinomun_mertebesi) Örnek:
Giriş 0 1 2 3
Çıkış 3 6 40 100
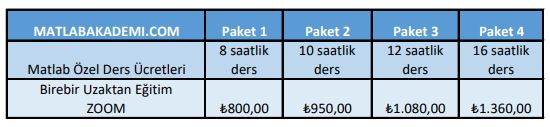  Giriş verilerini x satır vektörüne, çıkış verilerini ise y satır vektörüne atayalım. >> x = [0 1 2 3]; >> y = [3 6 40 100]; >> polyfit(x,y,3) ans = -0.8333   18.0000  -14.1667    3.0000 Sonuç olarak; y(x) = - 0.8333 x^3 + 18 x^2 - 14.1667 x + 3 elde ederiz. MATLAB AKADEMI MATLAB KURSU İÇİN TIKLAYIN. MATLAB ÖZEL DERSİ ALMAK İÇİN TIKLAYIN. ZOOM üzerinden online canlı özel ders için tıklayın.